一些数学函数在 GeoGebra 中的实际应用

这里的函数有些可能不是最简的，但它反映了思考的过程。对于函数的简化，如果有，则会出现在这里。

前言

曾经我遇到这样一个问题：有一个网站，每天去签到，第一天得 1 分、第二天得 2 分、第三天得 3 分，如此积累到 666 分需要多少天。
当时我想出来一条函数，实际上并不是一条，而是几条函数结合在一起的，算出来的结果大概是一个月，具体的天数我记不清了。
后来，更新了 GeoGebra 导致保存在 GeoGebra 里的函数丢失了，甚至我也想不起来当初的函数是怎么写的，只记得一部分，所以我打算将这些函数记录到这里。我记不住，但互联网有记忆。

函数

函数的绘制软件我推荐 GeoGebra。当然，这个软件还是有槽点的，比如计算的结果通常是小数而不是分数和带根号的数，这样一来有些计算变得麻烦了，不过现在没有更好的软件，有的话请告诉我。
前往 GeoGebra 官网

阅读体验欠佳！
该文章中有二维图像和三维图像导致性能下降。
调整函数后刷新或离开此网页会弹出提示框“可能未保存所做的更改。”，请直接点击“刷新”或“离开”。
手机端如需查看函数图像，请点击全屏按钮。

奇偶判断

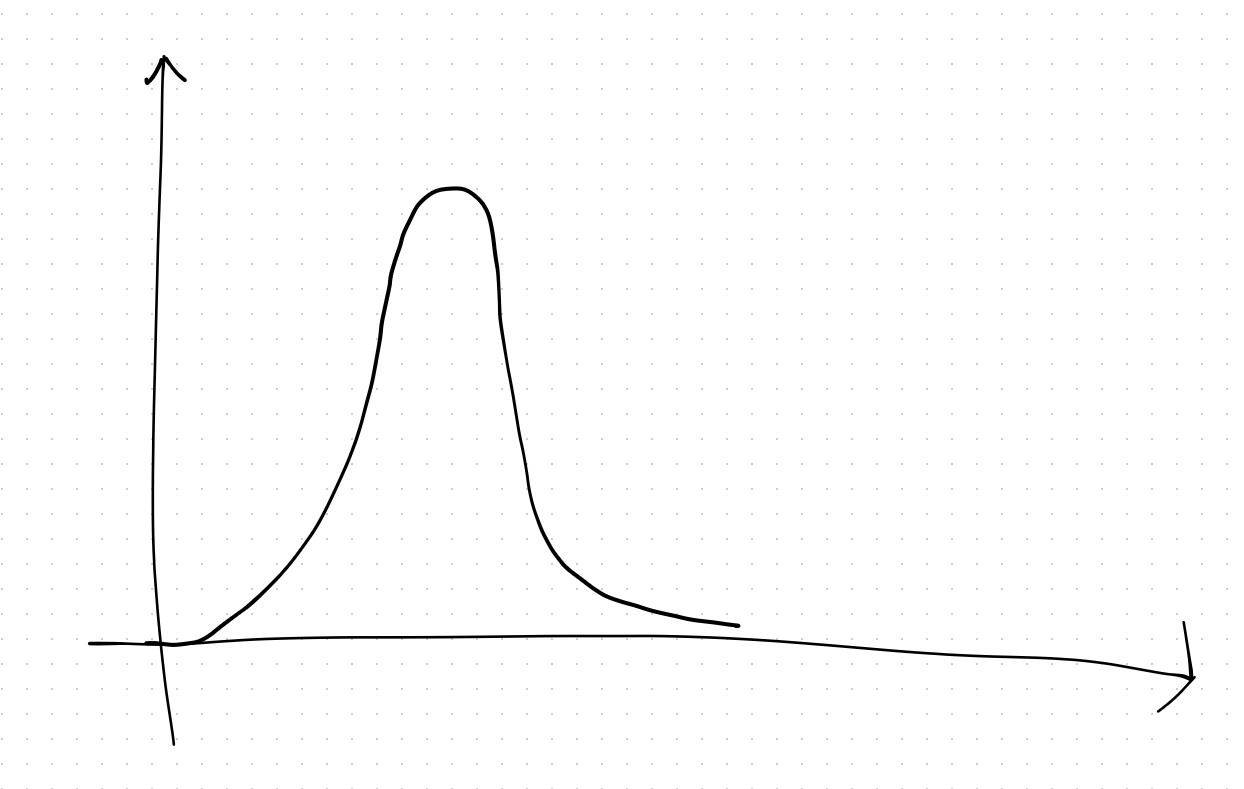
实际上方法有不少，这里我使用 $\sin $ 。

图像

这个函数会根据输入的 $x$ 的奇偶，当 $x$ 为奇数时输出 $1$，偶数时为 $0$，一般来讲就是用来乘的。如果需要偶数输出 $1$ ，奇数输出 $0$，那么就像 $g\left( x\right) $ 一样，把整个函数向左平移 $\dfrac{n}{2}$ 个单位就好了。
其实这个函数还需要限制 $x$ 为正整数的，不过这里就不写了，主要是方便后面使用。

正整数相加

这便是我在前言中所说的问题，想了好久想不出来，当初我是用了奇偶判断加其他好几条函数做出来的，那时出来的函数很长，看着图像我猜测是一元二次函数，结果呢…真就是啊。
我已经忘记以前是怎么解的了，那时闲麻烦不想求一元二次方程，虽然现在直接去求一元二次方程了，但心有不甘，还是很想还原出当时写出的式子的。

图像

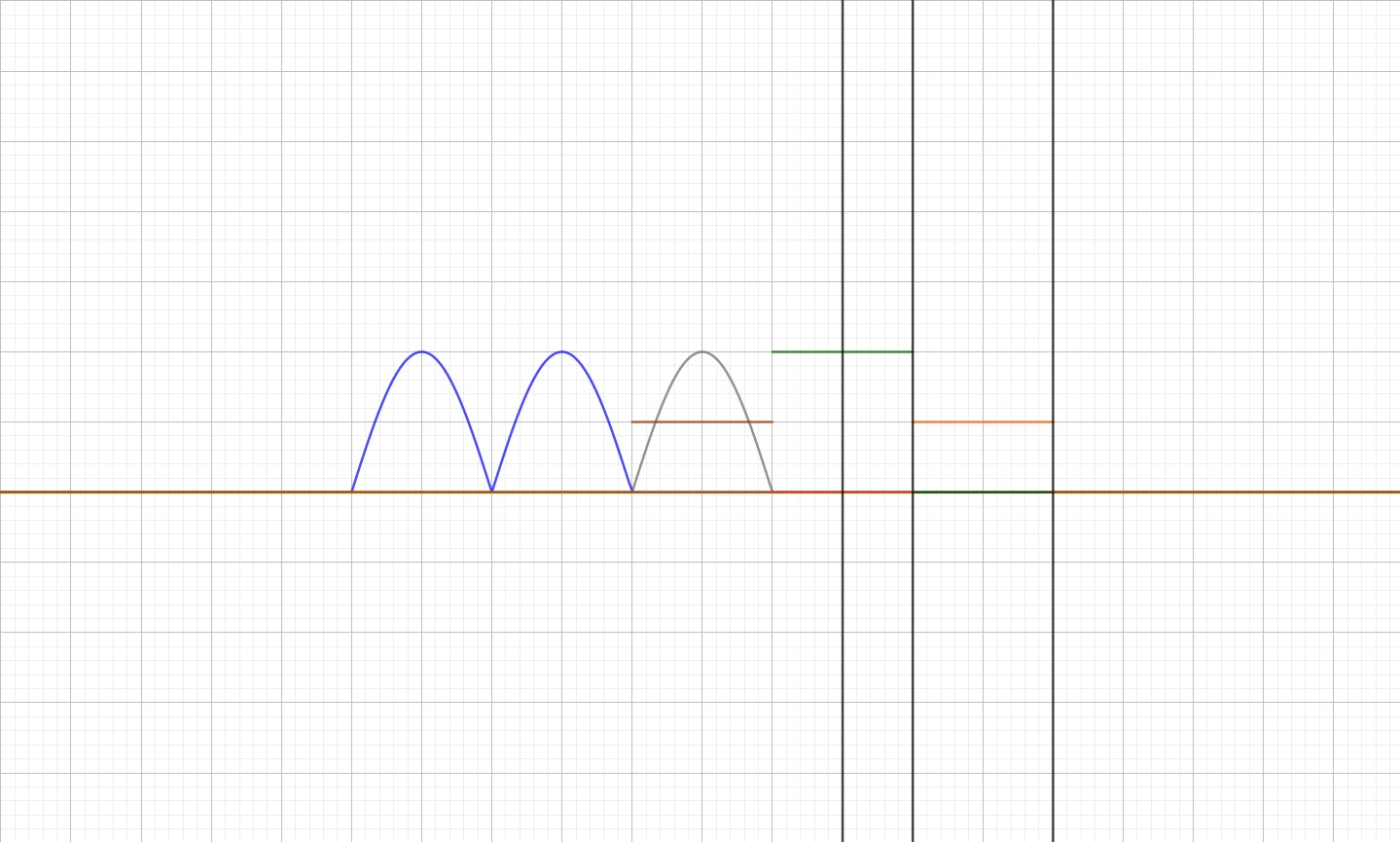
这里的 $f\left( x\right) $ 是直接带入三个点 $\left( 0,0\right)$ 、$\left( 1,1\right)$、$\left( 3,6\right)$ 解出来的，后面还带入了其他的点，最终确认了是这个函数。
不过 $f\left( x\right) $ 只能判断大于 $0$ 的部分，后面的 $-1$、$-2$、$-3$…… 只需要把这个函数的正半轴复制并旋转 $180^{\circ }$ 就行了，也就是 $g\left( x\right) $。
最后将两者合并得到 $q\left( x\right) $，这里的 $h$ 和 $p$ 这样写是因为有 bug。

至此，这个函数看似已经足够使用了。但是，还有一个问题有待解决，如果我是指定一个范围内的整数相加呢？
其实并不困难，首先定义两个变量，一个是起始，一个是结束，分别为 $a$ 和 $b$。此时，$a$ 必须小于或等于 $b$，且 $a$ 和 $b$ 都为整数。
分五种情况来看：

1. 当 $a$ 为 $0$
   此时就按照原始的函数去计算就行了。
2. 当 $a$ 大于 $0$
   这种情况下，无非是 $a-b$，所以也不复杂。
3. 当 $a$ 小于 $0$，$b$ 等于 $0$
   这种情况也不复杂，直接将 $a$ 带入到原始公式里就好了
4. 当 $a$ 小于 $0$，$b$ 小于 $0$
   那么就是 $a-b$。抽象一些，直接将 $a$ 和 $b$ 带入方程，得到两个长度不同的 $A$ 和 $B$，$B$ 整一段都是不需要的，而 $A$ 包含 $B$，所以把 $A$ 里的 $B$ 去掉就行。
5. 当 $a$ 小于 $0$，$b$ 大于 $0$
   这时就比较复杂了，根据我们上一种情况的抽象来看，$A$ 和 $B$ 都需要，所以就是 $b-a$

此时不应该直接“综上所述”得到一个多项式，我们再来观察一下。
根据上面的抽象方法，发现了什么没？
那就是当 $a$ 在正半轴时，$a$ 的部分是全都不需要的，只有在负半轴时是需要的。而 $b$ 正好相反过来。
而当 $a$ 在正半轴时，$a$ 是正数，负半轴时是负数，负数时是需要的，正数是不需要的，所以我们得到下面的函数 $c$。

图像

这里由于没有 $x$ 出现，GeoGebra 就没有把它当作一条函数来看待。
不过，GeoGebra 不仅可以渲染平面的图像，还可以渲染立体的图像，让我们来看看。其中 $a\left( x,y\right) $ 是我们要的函数。我还尝试过添加限制 $x\leq y$，不过嘛，效果不怎么样，各位可以把 $a\left( x,y\right) $ 给隐藏了，把 $b\left( x,y\right) $ 显示出来。点击函数左侧的圆就可以隐藏或显示。（疯狂掉帧ing…）

图像

抽取种类数

之前各种绕弯，那为什么我没想到阶乘即 $n\cdot \left( n-1\right) \cdot \left( n-2\right) \ldots \left( n-m+1\right)$ 。

所以现在的情况是两种，有要求顺序和没有要求顺序的。
在下面， $m$ 是总数， $n$ 是要抽取的数量。

当有序：

$A_{m}^{n}$

当无序：

$C_{m}^{n}$

弯路

懒惰促使我努力去寻找偷懒的方法。

在 $m$ 个东西里抽取 $n$ 个东西，不重复抽取，不考虑顺序，求有几种情况。
这个挺麻烦的，一上来就是一条立体函数。不过，我已经有思路了，我们先不要想象什么立体图形，就先想想其中一个平面。
我们假定 $m$ 是 $5$，$n$ 作为自变量，然后看看分别会有几种情况。
当 $n=1$ 时，有 $5$ 种；$n=2$，$10$；$n=3$，$10$；$n=4$，$5$；$n=5$，$1$。
发现没有，它是对称的，那么又来到求一元二次方程的时候了。
最终的结果是：$f\left( x\right) =-\dfrac{5}{2}x^{2}+\dfrac{25}{2}x-5$
由于我们要求的是立体函数，光这一条函数可不够用，还需要多几条来观察。
所以我们假定 $m=3$，所以 $g\left( x\right) =-2x^{2}+8x-2$
再假定 $m=4$，所以 $h\left( x\right) =-x^{2}+3x+1$

观察图像，乍一看没什么规律，又好像有点规律，那就是规律了但没完全规律。那就让我来讲讲到底规律了哪里。
首先，我们一直写得都是 $ax^{2}+bx+c$，这样写是为了计算起来方便，但我们还是需要把它们都变成 $a\left( x-h\right) ^{2}+k$ 这种顶点式。
好，现在来转换一下，得到下面的式子。

$p\left( x\right) =-\dfrac{5}{2}\left( x-\dfrac{5}{2}\right) ^{2}+\dfrac{85}{8}$
$q\left( x\right) =-2\left( x-2\right) ^{2}+6$
$r\left( x\right) =-\left( x-\dfrac{3}{2}\right) ^{2}+\dfrac{13}{4}$

然而还是没有什么用。可能是 $3$ 这个数太小了，所以我要尝试一下 $6$。
神奇的事情出现了，到了 $6$ 就出现了不管怎么算都对不上的情况，带入不同的点出现不同的式子…
（思索片刻）
这代表什么？这代表我们一开始的想法就是错的！它根本不是一元二次方程，只是因为前面的数刚好对上罢了。
将所有的点放到 GeoGebra 当中。（看上面的）

再次好好观察…
会发现它的图像更接近于这种。

看到的第一眼我想到了正态分布。嗯…虽然现在课本上还没讲过正态分布（不知道高二有没有），但我还是可以试一试的。
在百科上看到正态分布的定义后，已经感受到压力了，出现了我从没学过的 $\exp \left( \right) $，看来还要先会 $\exp \left( \right) $。
然后我又想偷懒了，不过还好 GeoGebra 里有“概率模式”，所以我打算尝试一下。

上来就是当头一棒，不仅有正态分布，还有其他的好多种分布，所以我打算利用其中的“二项分布”，看看能不能试出我要的（虽然我也不清楚我到底要什么）。

……
似乎我踏入了不应该踏入的领域。但既然来了，肯定要拿什么回去才行。

2021.09.12 更新

硬来不行，决定换一种方法。
那么，首先我们有两个必要的数，总数（total）和抽取量（extract），这两个是我在此处定义的。
总数和抽取量必须为非负整数，且抽取量不得大于总数。

定好限制之后，接下来开始计算有几种可能。
想起在平时我们怎么计算几种的，感觉有点类似冒泡算法，不过这里不需要排序，只需要每个都冒一遍就行了，整个冒的过程还可以简略。

在这里我们再引入一个“指”（point）的概念，即被“指”的需要被计数，粗略做了一个动画便于理解。

在实际操作中，“指”只会指向最后的几个“目标”（target）上，而它将会指向几个，我们可以通过总数减去倒数第二个“指”的未知来得到。
另外，我们还要检查当前“指”的数量，如果只有一个，则“目标”的数量直接统计起来。如果不止一个，我们需要让“指”进入下一层，直到剩余一个“指”才能统计数量。

可能有点过于抽象了，来举个例子。
现在总数定为 $4$。
当抽取量为 $1$ 时，此时抽取量为 $1$，剩余目标为 $4$，计算总数为 $4$。
当抽取量为 $2$ 时，此时抽取量不为 $1$，进入下一层，总数和抽取量各减去 $\left( 抽取量 - 1\right)$，此时抽取量为 $1$，总数为 $3$，即第一个总数为 $3$；回到上一层，此时最后一个指已经到最后一个目标了，因此倒数第二个（即第一个）指向后移动一次，同时最后一个指移动到倒数第二个指的后面一个目标上，此时总数为 $3$，抽取量为 $2$，老规矩，总数和抽取量各减去 $\left( 抽取量 - 1\right)$，然后就来到下一层，此时总数为 $2$，抽取量为 $1$，即计入总数 $2$，回到上一层，倒数第二个指向后移动，此时最后一个指无法移动，即倒数第二个指的计算已经结束。
剩下的如此类推……

将上面的用数字表示，0 是未被指向的目标，1 是被指向的目标，即：

4 > 1
1000
0100
0010
0001

4 > 2
1100
1010
1001
0110
0101
0011

4 > 3
1110
1101
1011
0111

4 > 4
1111

目前的思路到了这了，还在想怎么写成函数。

椭圆截线中点

这标题也太奇怪了吧……好吧，只是我想不出干练的标题罢了。

已知椭圆方程、椭圆截得直线线段中点坐标、直线方程中的任意两个、就可以求出另外一个

要求与参数：

• 椭圆方程为：$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$
• 中点坐标：$\left( x{0},y{0}\right) $
• 直线方程（点斜式）：$\left( y-y{0}\right) =k\left( x-x{0}\right) $

这原本是上课时老师在讲一道例题：已知椭圆方程、椭圆截得直线线段中点坐标，求直线方程。
当时看到老师的推理，我想着这应该可以化成一条式子吧，然后就去试了，具体的推理过程晚点放上来。

$$\left( y-y_{0}\right) =-\dfrac{b}{a}\cdot \dfrac{x_{0}}{y_{0}}\cdot \left( x-x_{0}\right)$$

其中，$k=-\dfrac{b}{a}\cdot \dfrac{x_{0}}{y_{0}}$